
![]() INTERVALOS
INTERVALOS

Una nota es un sonido con una determinada frecuencia. Por ejemplo la quinta cuerda de la guitarra, es decir la nota LA, tiene una frequencia de 110 Hz. La distancia relativa entre dos notas se denomina intervalo. El intervalo más pequeño se denomina semitono. Los intervalos reciben nombres especiales como "segunda mayor", "quinta justa", etc...
Una octava es el intervalo entre dos notas donde la frequencia de la nota más alta es el doble de la frecuencia de la nota más baja. Los nombres de las 12 notas que formarían el intervalo de una octava empezando desde la nota DO serían los siguientes:
DO, DO# o REb, RE, RE# o MIb, MI, FA, FA# o SOLb, SOL, SOL# o LAb, LA, LA# o SIb, SI, DO
En la tabla 1 se puede observar la denominación de todos los intervalos existentes dentro de una octava. La distancia vendrá expresada en semitonos.
|
Intervalos
|
Disminuida
|
Menor
|
Justa
|
Mayor
|
Aumentada
|
|
Segunda
|
0
|
1
|
2 ( 1 tono )
|
3
|
|
|
Tercera
|
2
|
3
|
4 ( 2 tonos )
|
5
|
|
|
Cuarta
|
4
|
5 ( 2'5 tonos )
|
6
|
||
|
Quinta
|
6
|
7 ( 3'5 tonos )
|
8
|
||
|
Sexta
|
7
|
8
|
9 ( 4'5 tonos )
|
10
|
|
|
Séptima
|
9
|
10
|
11 ( 5'5 tonos )
|
12
|
|
|
Octava
|
11
|
12 ( 6 tonos )
|
13
|
- Tabla 1 -
Muchas veces nos encontramos con fórmulas del siguiente tipo : 1 b3 5 b7. ¿Qué quiere decir esta fórmula?, ¿a qué está haciendo referencia?. Pues simplemente es una forma abreviada de describir los intervalos que se deben cumplir. La relación entre esa notación y los intervalos es la siguiente:
|
DO
|
|
MI
|
|
SOL
|
|
SI
|
|
RE
|
|
FA
|
|
LA
|
|
DO
|
|
1
|
|
3
|
|
5
|
|
7
|
|
9
|
|
11
|
|
13
|
|
15
|
|
|
«MAYOR»
|
«menor»
|
«MAYOR»
|
«menor»
|
«menor»
|
«MAYOR»
|
«menor»
|
|
Pero ¿cómo recordar cuál es la distancia y nombre de cada intervalo?. ¿Por qué por ejemplo el intervalo segunda mayor tiene que tener 1 tono?. Bueno pues todos estos intervalos se podrán recordar fácilmente si calculamos la distancia desde la nota DO hasta cualquiera de las notas sucesivas a ella, tal y como se ilustra en la tabla 2.
|
Grado Escala |
Semitonos |
Tonos
|
Nombre del intervalo
|
Ejemplo
|
|
I
|
0
|
0
|
Unísono
|
C-C
|
|
II
|
2
|
1
|
Segunda Mayor
|
C-D
|
|
III
|
4
|
2
|
Tercera Mayor
|
C-E
|
|
IV
|
5
|
2'5
|
Cuarta justa
|
C-F
|
|
V
|
7
|
3'5
|
Quinta justa
|
C-G
|
|
VI
|
9
|
4'5
|
Sexta mayor
|
C-A
|
|
VII
|
11
|
5'5
|
Séptima mayor
|
C-B
|
|
I
|
12
|
6
|
Octava
|
C-C
|
- Tabla 2 -
A continuación se va a observar la aplicación de los intervalos para un instrumento en concreto, la guitarra:
|
|
|
INTERVALO: DO-RE 1 tono ( 2 semitonos) SEGUNDA MAYOR |
|
|
|
INTERVALO: DO-MI 2 tonos ( 4 semitonos) TERCERA MAYOR |
|
|
|
INTERVALO: DO-FA 2 1/2 tonos ( 5 semitonos) CUARTA JUSTA |
|
|
|
INTERVALO: DO-SOL 3 1/2 tonos (7 semitonos) QUINTA JUSTA |
|
|
|
INTERVALO: DO-LA 4 1/2 tonos (9 semitonos) SEXTA MAYOR |
|
|
|
INTERVALO: DO-SI 5 1/2 tonos (11 semitonos) SÉPTIMA MAYOR |
|
|
|
INTERVALO: DO-DO 6 tonos (12 semitonos) OCTAVA |
- Figura 1 -
Todos estos patrones se podrán aplicar entre cualquier par de cuerdas excepto cuando se esté en el caso de tercera y segunda cuerda. Esto es debido a la propia afinación de la guitarra tal y como se muestra en la figura 2.
- Figura 2 -
Por tanto habrá que aumentar un traste en la segunda cuerda para hacer una correspondencia con los intervalos vistos en la figura 1.
|
|
|
INTERVALOS |
- Figura 3 -
En la figura 4 se podrá observar un mapeado completo de los intervalos. Las notas rodeadas con el círculo indican la tónica, por tanto se podrá tomar como tónica cualquier nota. En la imagen se ha considerado como tónica la nota DO ( octavo traste sexta cuerda).
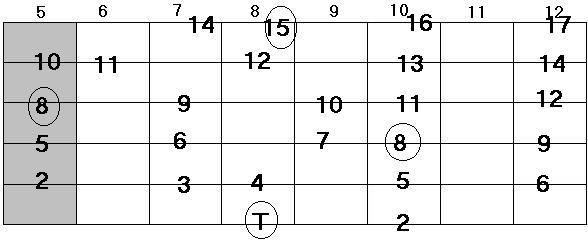
- Figura 4 -
Los intervalos también pueden verse de la siguiente manera
|
DO
|
RE
|
MI
|
FA
|
SOL
|
LA
|
SI
|
|
T
|
2
|
3
|
4
|
5
|
6
|
7
|
|
8(T)
|
9 (= intervalo 2ª)
|
10
|
11
|
12
|
13
|
14
|
|
1 Tono
|
1 Tono
|
1/2 Tono
|
1 Tono
|
1 Tono
|
1 Tono
|
|
|
2 Tonos
|
||||||
|
2'5 Tonos
|
||||||
|
3'5 Tonos
|
||||||
|
4'5 Tonos
|
||||||
|
5'5 Tonos
|
||||||
|
6'5 Tonos
|
||||||
- Figura 5 -